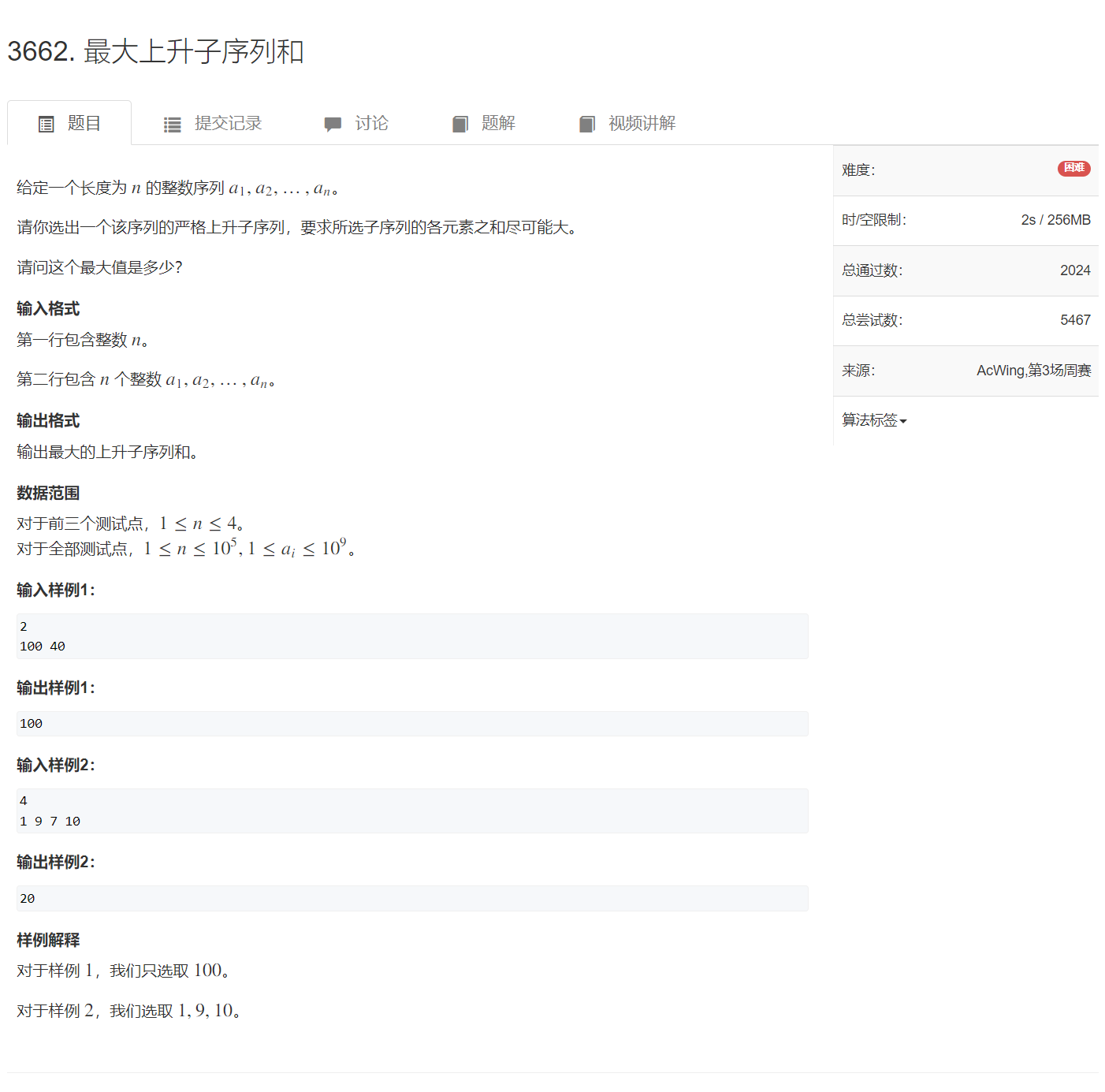
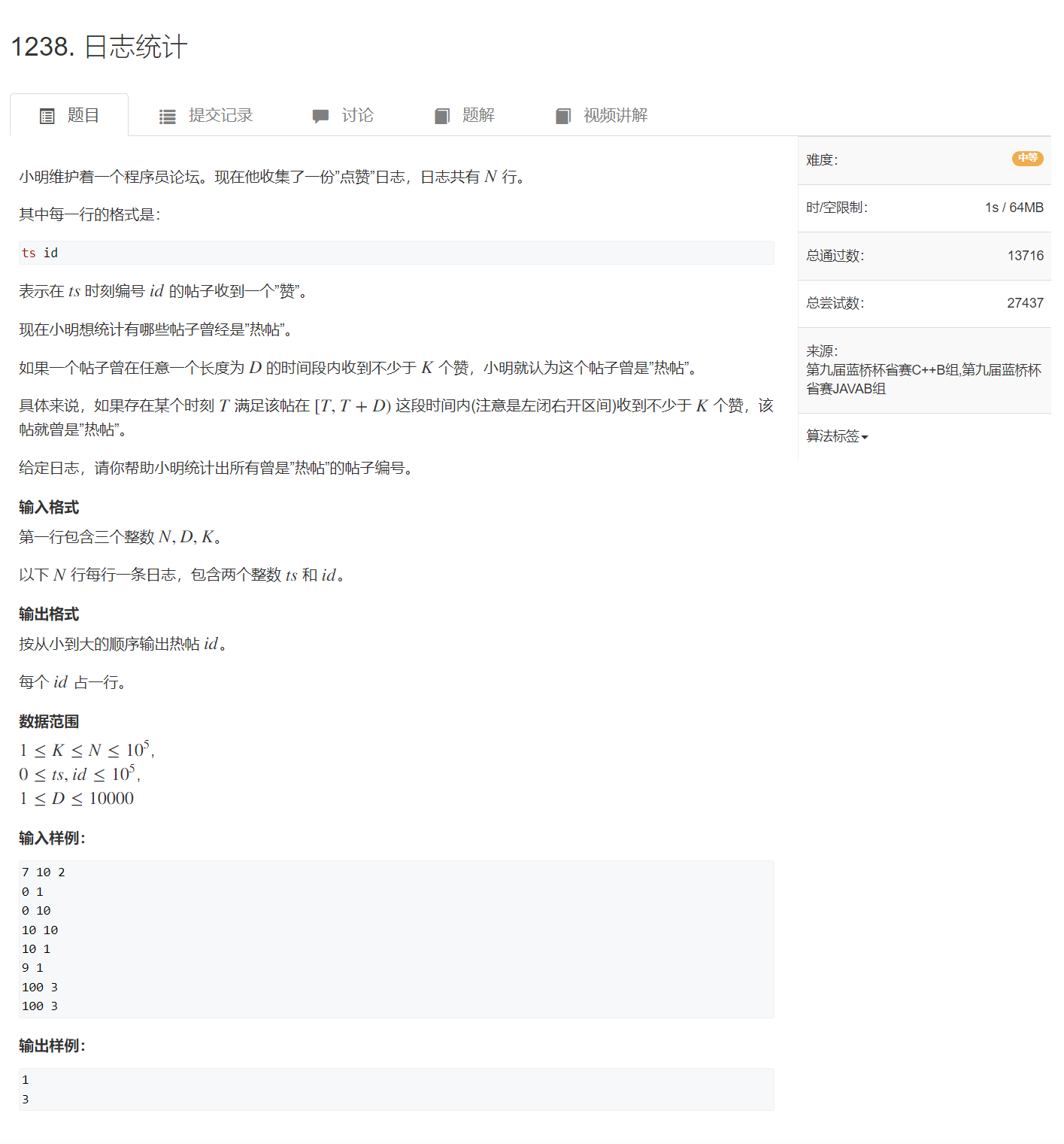
原题链接

前置知识

1. 离散化

2. 树状数组 or 线段树 （用于维护前缀的信息）

3. 最长上升子序列 AcWing 895. 最长上升子序列

分析

首先这道题在不考虑优化的情况下是一道最长上升子序列板子题，不会的先去看一下这道题，由于本题数据范围过大，我们需要考虑如何优化，这也是本题的难点所在。

我们先从DP的角度讨论一下这题的朴素写法

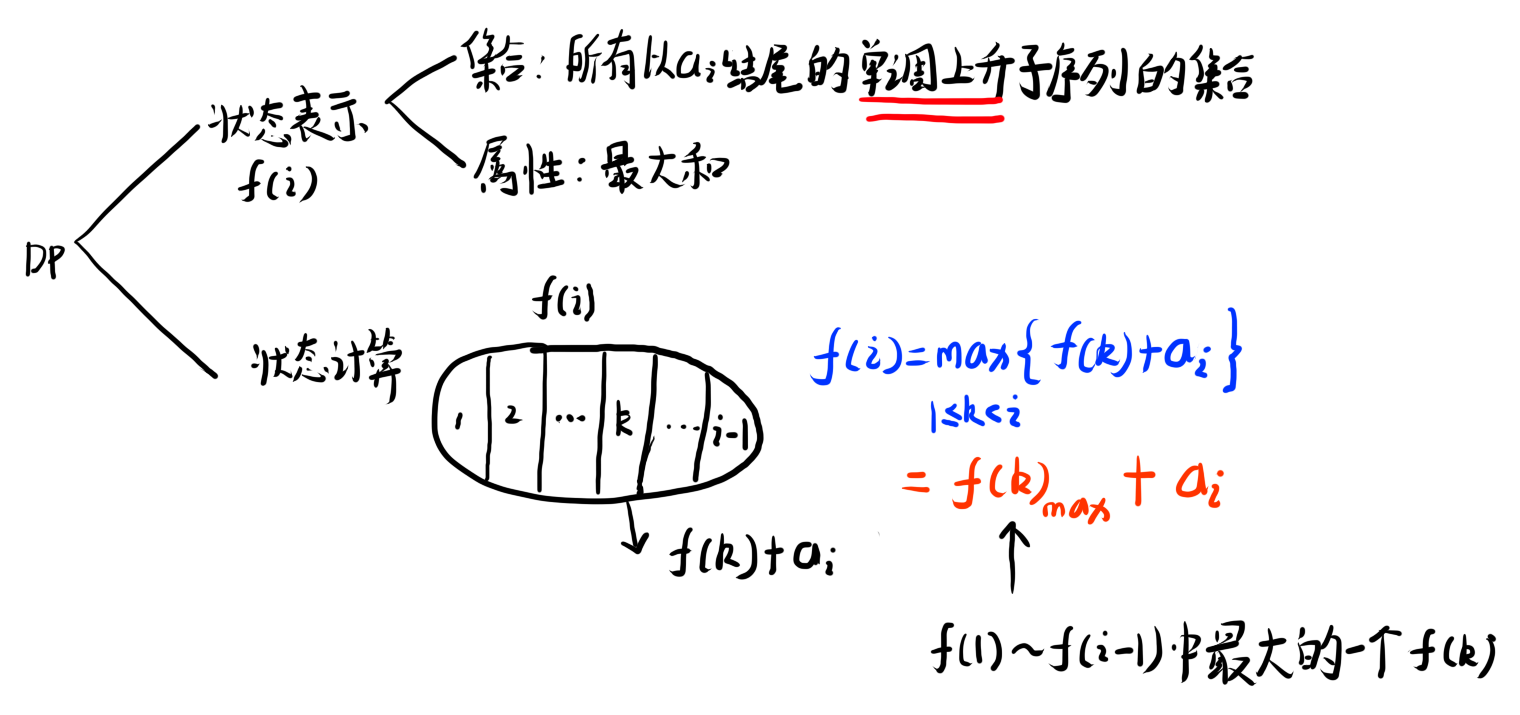
本题的状态转移方程见上图，显然，我们在执行状态方程的途中需要寻找某一个前缀的最大值，这使得我们每次执行方程都会遍历一遍前面的每一个数，这就导致了$O(n^2)$的时间复杂度，我们需要考虑一下如何将这一维优化掉。

由于我们每次寻找的$f(k)_{max}$是一个前缀中的最大值，我们很容易可以想到树状数组或者线段树，来动态的维护前缀的最大值吗，这样我们每次查询就可以从$O(n)$优化到$O(logn)$

那么我们如何来维护这样一个前缀呢？

比较容易想到的是将$f(i)$维护到下标$i$，如下图所示

但是这样做在本题中是否行得通呢？

先说结论，本题不可以这样维护，由于题目明确规定，我们要找的子序列为单调上升子序列，所以必须满足一个条件$a_i>a_k$，如果我们维护上面这样一个关系，虽然可以让我们找到前缀中最大的一个$f(k)$，但是我们却无法保证$a_i>a_k$。

那我们如何维护呢？

我们考虑将$f(i)$维护到下标$a_i$，如下图所示

如果我们采取这种维护策略，若$a_2>a_i$，则我们在查询$a_i$的前缀时，就永远也无法找到$f(2)$，这样就保证了$a_i>a_k$这个条件始终是成立的。

但是，到这里还有最后一个问题，$1≤a_i≤10^9$，如果我们直接维护，那么需要开一个大小为$10^9$的数组才可以做到，这显然是不可以接受的，同时我们发现$1≤n≤10^5$，这说明我们可以离散化一下，把每一个$a_i$按照相对位置关系，一一映射到$1≤n≤10^5$这个区间上，若文字难以理解，可以看下面的图。

离散化需要去重，由于本题的答案是取决于单调上升子序列并且子序列内部元素不能相等，所以去重不影响答案，我们需要的只是每个元素的相对位置不变，以及相对位置信息。

代码

如下我将分享朴素写法，树状数组，线段树三种写法

朴素做法 时间复杂度:$O(n^2)$

#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
const int N = 1e5 + 10;
int n,a[N];
LL f[N];

int main()
{
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i],f[i] = a[i];
    
    for(int i=1;i<=n;i++)
        for(int k=1;k<i;k++)
            if(a[i]>a[k]) f[i] = max(f[i],f[k]+a[i]);
    
    LL res = 0;
    for(int i=1;i<=n;i++) res = max(res,f[i]);
    cout<<res<<endl;
    return 0;
}

树状数组优化 时间复杂度$O(nlogn)$

#include <bits/stdc++.h>
#define lowbit(x) (x)&(-x)
using namespace std;

typedef long long LL;
const int N = 1e5 + 10;
int n,m,a[N];
vector<int> g;
LL f[N],tr[N];

void add(int x,LL c)
{
    for(int i=x;i<=m;i+=lowbit(i)) tr[i] = max(tr[i],c);
}

LL query(int x)
{
    LL res = 0;
    for(int i=x;i;i-=lowbit(i)) res = max(res,tr[i]);
    return res;
}

int main()
{
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i],g.push_back(a[i]);
    
    //离散化
    sort(g.begin(),g.end());
    g.erase(unique(g.begin(),g.end()),g.end());
    m = g.size(); //离散化之后的下标最大数
    
    for(int i=1;i<=n;i++)
    {
        int x = lower_bound(g.begin(),g.end(),a[i]) - g.begin() + 1; //离散化之后的下标
        f[i] = query(x-1) + a[i]; //状态转移
        add(x,f[i]);
    }
    
    LL res = 0;
    for(int i=1;i<=n;i++) res = max(res,f[i]);
    cout<<res<<endl;
    return 0;
}

线段树优化 时间复杂度$O(nlogn)$

#include <bits/stdc++.h>
#define lowbit(x) (x)&(-x)
#define ls u<<1
#define rs u<<1|1
#define Mid(x,y) (x+y)>>1
using namespace std;

typedef long long LL;
const int N = 1e5 + 10;
int n,m,a[N];
vector<int> g;
LL f[N];

struct Node
{
    int l,r;
    LL v;
}tr[4*N];

void pushup(int u)
{
    tr[u].v = max(tr[ls].v,tr[rs].v);
}

void build(int u,int l,int r)
{
    tr[u] = {l,r};
    if(l==r) return;
    int mid = Mid(l,r);
    build(ls,l,mid),build(rs,mid+1,r);
}

void modify(int u,int x,LL v)
{
    if(tr[u].l==x&&tr[u].r==x)
    {
        tr[u].v = v;
        return;
    }
    int mid = Mid(tr[u].l,tr[u].r);
    if(x<=mid) modify(ls,x,v);
    else modify(rs,x,v);
    pushup(u);
}

LL query(int u,int l,int r)
{
    if(tr[u].l>=l&&tr[u].r<=r) return tr[u].v;
    int mid = Mid(tr[u].l,tr[u].r);
    LL v = 0;
    if(l<=mid) v = query(ls,l,r);
    if(r>mid) v = max(v,query(rs,l,r));
    return v;
}

int main()
{
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i],g.push_back(a[i]);
    
    //离散化
    sort(g.begin(),g.end());
    g.erase(unique(g.begin(),g.end()),g.end());
    m = g.size(); //离散化之后的下标最大数
    
    build(1,1,m); //建树
    
    for(int i=1;i<=n;i++)
    {
        int x = lower_bound(g.begin(),g.end(),a[i]) - g.begin() + 1; //离散化之后的下标
        if(x>1) f[i] = query(1,1,x-1) + a[i]; //状态转移
        else f[i] = a[i];
        modify(1,x,f[i]);
    }
    
    LL res = 0;
    for(int i=1;i<=n;i++) res = max(res,f[i]);
    cout<<res<<endl;
    return 0;
}