原题链接

分巧克力.png

一道蓝桥杯真题关于二分的思考

二分问题的难点一共有两个，一个是确定二分边界，也就是选择两个二分模板中的其中一个，另一个则是如何设计cheak()函数，使得二分区间可以由某种性质一分为二。

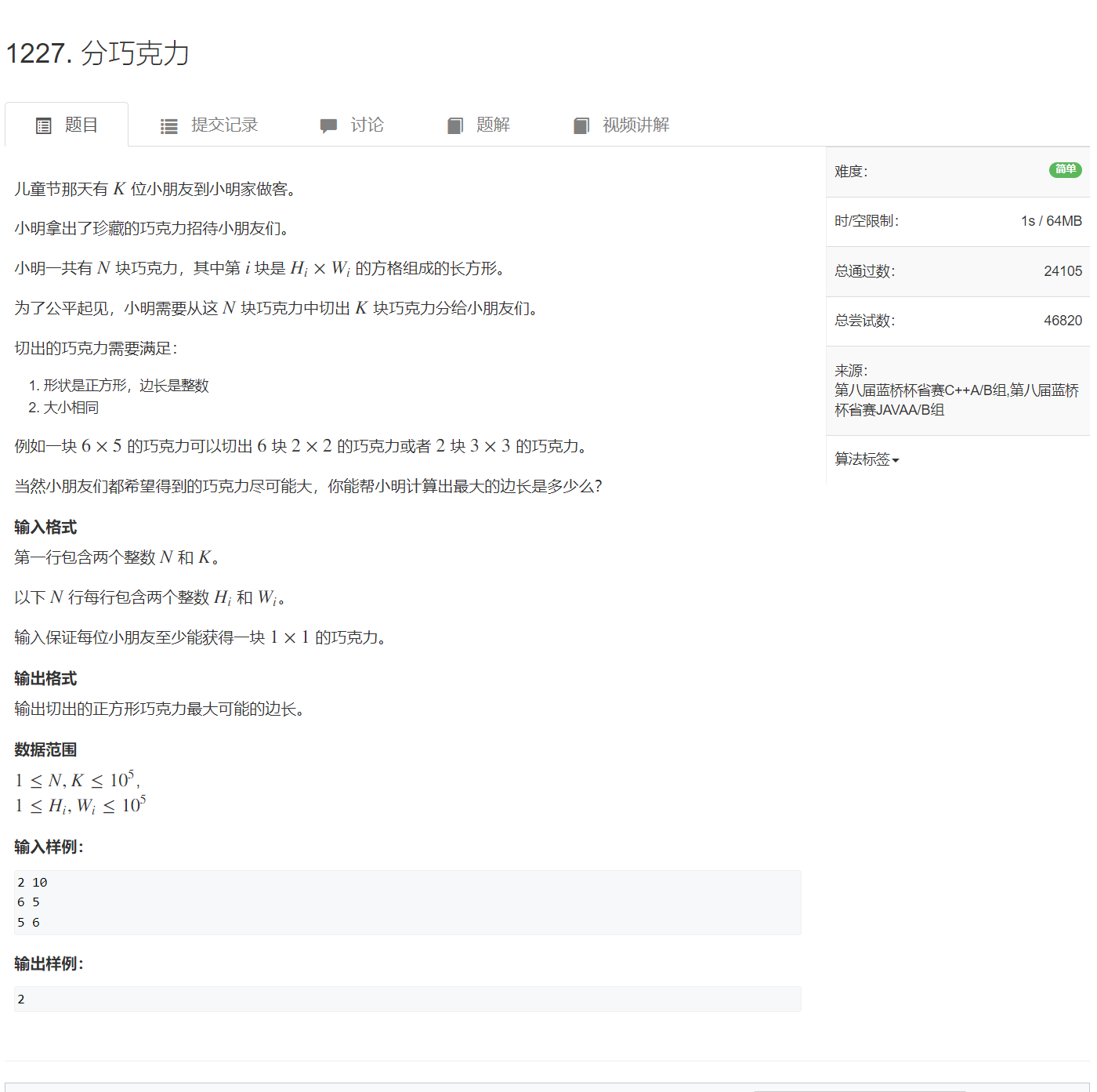
1.题目

题目描述

儿童节那天有$ K $位小朋友到小明家做客。

小明拿出了珍藏的巧克力招待小朋友们。

小明一共有$ N $块巧克力，其中第$ i $块是$ H_i×W_i $的方格组成的长方形。

为了公平起见，小明需要从这$ N $块巧克力中切出$ K $块巧克力分给小朋友们。

切出的巧克力需要满足：

1.形状是正方形，边长是整数
2.大小相同

例如一块$ 6×5 $的巧克力可以切出$ 6 $块$ 2×2 $的巧克力或者$ 2 $块$ 3×3 $的巧克力。

当然小朋友们都希望得到的巧克力尽可能大，你能帮小明计算出最大的边长是多少么？

输入格式

第一行包含两个整数$ N $和$ K $。

以下 N 行每行包含两个整数$ H_i $和$ W_i $。

输入保证每位小朋友至少能获得一块$ 1×1 $的巧克力。

输出格式

输出切出的正方形巧克力最大可能的边长。

数据范围

$ 1≤N,K≤10^5 $,
$ 1≤H_i,W_i≤10^5 $

输入样例

2 10
6 5
5 6

输出样例

2.前置知识（二分查找）

二分查找简单来说，就是某个区间满足某种性质，并且存在一个边界可以把这个区间一分为二，使得左边区间满足某种性质，同时右边区间也满足某种性质。而这个边界通常就是我们要查找的答案，它可以由题意，以及我们自己的理解和分析定义。

二分模板（向左边查找---更新右端点）

//l:区间左端点 r:区间右端点
while(r > l)
{
    int mid = r + l >> 1;
    if(cheak(mid)) r = mid; //如果cheak(mid)满足边界右边区间的性质，那么答案在mid的左边我们更新右端点
    else l = mid + 1; //注意此处为 mid + 1
}

二分模板（向右查找---更新左端点）

//l:区间左端点 r:区间右端点
while(r > l)
{
    int mid = l + r + 1 >> 1; //注意要加一上取整 防止mid等于左端点 陷入死循环
    if(cheak(mid)) l = mid; //如果cheak(mid)满足边界左边区间的性质，那么答案在mid的右边我们更新左端点
    else r = mid - 1; //注意此处为 mid - 1
}

3.分析

具体题意请看上述原题，很显然我们的目的是在区间$ 1≤x≤max(H_i,W_i) $内确定一个最大的边长$ x $，使得第$ i $块巧克力可以分成若干小块（注意不可拼接），所有巧克力的若干小块加起来的数量恰好等于$ k $。那么这个$ x $就是我们最后的答案。

那么我们怎么才能找到这个$ x $呢？

通过观察我们发现，巧克力最后分成的总块数$ k $和边长$ x $具有一定关系，当$ x $越大，我们最终分得的小巧克力块数$ k $就越小。

换句话说就是，在区间$ 1≤x≤max(H_i,W_i) $中，边长的大小与最终分得的小巧克力块数$ k $成反比关系。

既然我们最终要求的答案$ x $恰好和$ k $有关，并且答案所在的区间又刚好可以由$ k $一分为二成两种不同的性质，因此本道题可以使用二分，$ k $就是我们要找的二分边界,左边的性质我们可以描述为$ cheak(x)≥k $，也就是说左边区间内的边长所分得的小巧克力总块数要大于等于题目要求的块数，因此我们可以由此更新左端点，使得答案区间向右边缩小，这样不仅可以求得更大的边长$ x $，也可以找到恰好满足题意的$ k $。

由上面的分析，我们知道本题需要向右查找，因此我们选择模板二(请看前置知识)。

加上基本的数据输入，很容易我们可以得到如下代码

#include <bits/stdc++.h>
using namespace std;

typedef pair<int,int> PII;
const int N = 1e5 +10;
int n,k;
PII a[N];

int main()
{
    cin>>n>>k;
    for(int i=1;i<=n;i++) cin>>a[i].first>>a[i].second;

    int l = 1,r = 1e5;
    while(r > l)
    {
        int mid = l + r + 1 >> 1;
        if(cheak(mid)) l = mid; //注意此时cheak()还并没有定义
        else r = mid - 1;
    }
    cout<<l<<endl;
    return 0;
}

这样，我们的问题就得到了进一步简化，变成了如何设计$ cheak() $函数，使得$ cheak(mid) $可以刚好满足边界$ k $的左边区间性质，这样我们便可以顺理成章的更新左端点，使得整个二分向右查找，最总找到我们所需要的答案$ x $。
由上面的图示，我们可以知道，边界左边区间的性质刚好就是所分得的小巧克力总块数，因此我们的$ cheak() $可以设计为如下

bool cheak(int x)
{
    int res = 0; //所分得的小巧克力总块数
    for(int i=1;i<=n;i++) //遍历每一个大巧克力
    {
        res += (a[i].first/x) * (a[i].second/x);  //计算累加每一个大巧克力可以分多少个小巧克力
        if(res>=k) return true; //如果满足边界左边区间性质 返回true
    }
    return false; //否则返回false
}

4.总代码二分查找时间复杂度$ O(nlogn) $

#include <bits/stdc++.h>
using namespace std;

typedef pair<int,int> PII;
const int N = 1e5 +10;
int n,k;
PII a[N];

bool cheak(int x)
{
    int res = 0; //所分得的小巧克力总块数
    for(int i=1;i<=n;i++) //遍历每一个大巧克力
    {
        res += (a[i].first/x) * (a[i].second/x);  //计算累加每一个大巧克力可以分多少个小巧克力
        if(res>=k) return true; //如果满足边界左边区间性质 返回true
    }
    return false; //否则返回false
}

int main()
{
    cin>>n>>k;
    for(int i=1;i<=n;i++) cin>>a[i].first>>a[i].second;

    int l = 1,r = 1e5;
    while(r > l)
    {
        int mid = l + r + 1 >> 1;
        if(cheak(mid)) l = mid; //注意此时cheak()还并没有定义
        else r = mid - 1;
    }
    cout<<l<<endl;
    return 0;
}